An open vessel is in the shape of a right-circular cone of semi-vertical angle 45 with axis
Question:
An open vessel is in the shape of a right-circular cone of semi-vertical angle 45° with axis vertical and apex downwards. At time t = 0 the vessel is empty. Water is pumped in at a constant rate pm3s–1 and escapes through a small hole at the vertex at a rate kym3s–1, where k is a positive constant and y is the depth of water in the cone. Given that the volume of a circular cone is πr2h/3, where r is the radius of the base and h its vertical height, show that
![]()
Deduce that the water level reaches the value y = p/(2k) at time
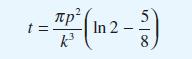
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





