Question: Solve the differential equation obtained in Example 8.4 to determine the amount x(t) of salt in the tank at time t minutes. Initially the tank

Solve the differential equation

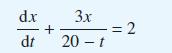
dx dt + 3x 20 - t = 2 ||

obtained in Example 8.4 to determine the amount x(t) of salt in the tank at time t minutes. Initially the tank contains pure water.

Data from Example 8.4

Suppose that a tank initially contains 80 litres of pure water. At a given instant (taken to be t = 0) a salt solution containing 0.25 kg of salt per litre flows into the tank at a rate of 8 litres min^–1. The liquid in the tank is kept homogeneous by constant stirring. Also, at time t = 0 liquid is allowed to flow out from the tank at a rate of 12 litres min^–1. Show that the amount of salt x(t) (in kg) in the tank at time t (min) ≥ 0 is determined by the mathematical model

dx dt + 3x 20 - t = 2 ||

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

We find that the appropriate initial condition is x0 0 Hence we have the dif... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

In Excel Function formatting Betting Assignment Write an IF statement with the description here The random # you roll is the number you pick you win. Winnings formula in Excel would be something like...

a. Example 13-1: Batch Reactor with an Exothermic Reaction Wolfram 1. Adiabatic Case: Use Wolfram to see whether you can find a trajectory that is ready to ignite and whose trajectory looks like a...

2. [011 Points] DETAILS PREVIOUS ANSWERS ZILLDIFFEQMODAP11 1.3.002. MY NOTES ASK YOUR TEACHER The population model given in (1) in Section 1.3 . P or f = 1:.\" (1) dt or fails to take death into...

Name: ________________________ Class: ___________________ Date: __________ Final Exam for Math 193 1. a) Evaluate the integral. 20xe 5x dx b) Evaluate the integral. 81 t ln tdx 1 c) Evaluate the...

4. (45 points) Two large tanks A and B are interconnected. Initially, tank A contains 24 liters of brine which contains 5 kg of dissolved salt and tank B contains 24 liters of brine in which 2 kg of...

Differential Equations proficient (only ). Please see the question below and thank you ahead of time. 38. Consider the cascade of two tanks shown in Fig. 1.5.5. with Vi = 100 (gal) and V2 = 200 (gal)...

Consider the cascade of two tanks of brine shown in the figure below, with V = 110 gallons and V = 194 gallons being the volumes of brine in the two tanks. Each tank also initially contains 47 lb of...

Q1) Solve the differential equation (y^(13) x )(dy)/(dx) = 1 + x. use the initial condition y(1)=3 , express y^14 in terms of x Q2) find the function y=y(x) for x>0 (dy)/(dx) = (2 + 12 x)/(xy^2) x >...

A tank contains 50 litres of pure water. At time t = 0, saltwater of concentration 2 kilograms of salt per litre is poured into the tank at a rate of 10 litres per minute, mixed thoroughly, and then...

Find the temperature distribution in a metal rod of length 1 m as shown in Figure i that is initially at 70 C. The steady-state temperature at the left and right ends of the rod are given by 50C and...

Explain the difference between a floating lien and a trust receipts arrangement.

If an organization deals successfully with change and has created procedures and systems that can be adjusted to the environment, the existing security improvement program will probably continue to...

4 Explain how firms can enhance customer satisfaction.

Determine the moments at Band D, then draw the moment diagram. Assume A and C are pinned and B and D are fixed connected. EI is constant. 8k -10 ft- 10 ft- -15 ft- 12 ft

Determine the moment that each member exerts on the joint at B, then draw the moment diagram for each member of the frame. Assume the support at A is fixed and C is a pin. EI is constant. 2 k/ft 6 ft...

Determine the moment that each member exerts on the joint at B, then draw the moment diagram for each member of the frame. Assume the supports at A, C, and D are pins. EI is constant. 6 m 6 m. 8 m 12...

Calculate the amount of fair premium. A. Between 300 and 310 B. Between 310 and 320 C. Between 320 and 330 D. None of the above

As firms grow, should they have division of labor and add staff positions? Give examples with your answer.

A mortgage-backed security SPV issues a total of $150M of tranched debt: The senior layer contains $100M at an interest rate of LIBOR + 0.5%. The subordinated layer contains $30M at a rate of LIBOR +...