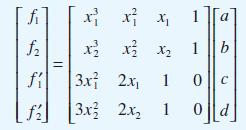
Data is fitted to a cubic f ax 3 bx 2 cx d with the slope of the curve given by f ' 3ax 2 2bx c If f 1 f(x 1 ), f 2 f(x 2 ), f ' 1 f '(x 1 ) and f 2 f(x 2 ), show that fitting the data gives the matrix equation for a, b, c and d as Use Gaussian elimination to evaluate a, b, c and d For the case eva...

Fitting the data to the cubic approximation to f and f gives the matr ...

Data is fitted to a cubic f = ax 3 + bx 2 + cx + d

Question:

Data is fitted to a cubic f = ax³ + bx² + cx + d with the slope of the curve given by f' = 3ax² + 2bx + c If f₁ = f(x₁), f₂ = f(x₂), f '₁ = f'(x₁) and f´₂ = f´(x₂), show that fitting the data gives the matrix equation for a, b, c and d as

fi f || x 2 x 2 x 2x 3x2x 1 0 3x 1 a b 1 0 C d

Use Gaussian elimination to evaluate a, b, c and d. For the case

X 0.4 0.8 f 0.327 54 0.404 90 0.511 73 -0.054 14

evaluate a, b, c and d. Plot the cubic and estimate the maximum value of f in the region 0 1. Note that this exercise forms the basis of one of the standard methods for finding the maximum of a function f(x) numerically.

Fantastic news! We've Found the answer you've been seeking!