Equation (10.3), arising from the model of the take-off run of an aircraft developed, can be solved

Question:

Equation (10.3), arising from the model of the take-off run of an aircraft developed, can be solved by the techniques introduced in Exercises 24 and 26. Assuming that the thrust is constant, find the speed of the aircraft as a function both of time and of distance run along the ground. The take-off speed of the aircraft is denoted by V2. Find expressions for the length of runway required and the time taken by the aircraft to become airborne in terms of take-off speed.

Equation 10.3

ds dt m- ( ) - ds dt 2 = T - mg (10.3)

Data from Question 26

Show that by making the substitution

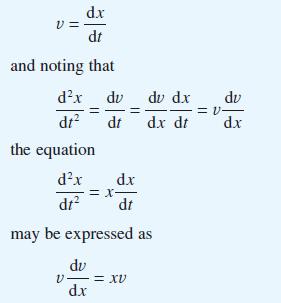
d.x dt and noting that dx du dt dt the equation dx dt may be expressed as v= du dx d.x -X = || ax=a dt du dx

Show that the solution of this equation is v = 1/2x² + C and hence find x(t). This technique is a standard method for solving second-order differential equations in which the independent variable does not appear explicitly. Apply the same method to obtain the solutions of the differential equations

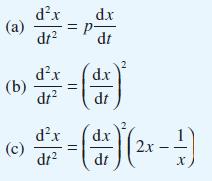
(a) (b) (2) dx TIP X-P dt X-P ZIP || || xp -d dt Xp dt = (dr) (x - - ) |2x

Data from Question 24

Show that by making the substitution

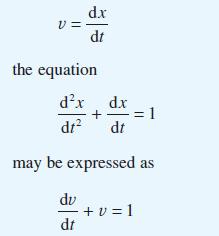
V = d.x dt the equation dx dt ap + dx dt may be expressed as = 1 - + v = 1 dt

Show that the solution of this equation is v = 1 + Ce^–t and hence find x(t). This technique is a standard method for solving second-order differential equations in which the dependent variable itself does not appear explicitly. Apply the same method to obtain the solutions of the differential equations

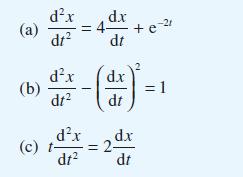
dx d.x (a) = 4 dt dt (b) dx dt dx (c) t- d.x dt +e-1 dt dt el = 2dx = 1