Show that by making the substitution Show that the solution of this equation is v = 1/2x
Question:
Show that by making the substitution
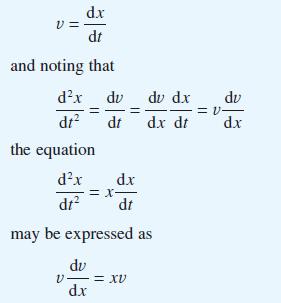
Show that the solution of this equation is v = 1/2x2 + C and hence find x(t). This technique is a standard method for solving second-order differential equations in which the independent variable does not appear explicitly. Apply the same method to obtain the solutions of the differential equations
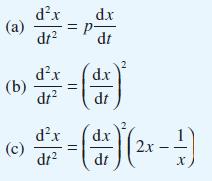
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





