Show that the differential is not exact, but that a constant m can be chosen so that

Question:

Show that the differential

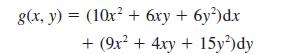
g(x, y) = (10x + 6xy + 6y)dx +(9x + 4xy + 15y) dy

is not exact, but that a constant m can be chosen so that

is equal to dz, the exact differential of a function z = f(x, y). Find f(x, y).

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

Modern Engineering Mathematics

ISBN: 9781292253497

6th Edition

Authors: Glyn James

See More Books

Question Posted: Jan 17, 2024 03:01 AM

See More Questions

Let (x) be a function of one variable defined near x = a. Given a number M, set e(x) = f(x) - L(x) e(x) L(x) = f(a) + M(x a), Thus, f(x)=L(x) + e(x). We say that f is differentiable at x =a if M can...
KYC's stock price can go up by 15 percent every year, or down by 10 percent. Both outcomes are equally likely. The risk free rate is 5 percent, and the current stock price of KYC is 100. (a) Price a...
1. describe your philosophy of HR, specifically addressing the balance between an HR employee's responsibility to represent the company and the responsibility to advocate for team members. 2....
The following information has been extracted from the financial statements of XYZ Ltd for the year ended 31 December 2022: Income Statement Sales revenue: $3,000,000 Cost of goods sold: $1,200,000...
The velocity field given in Prob. 2.4 is called vortex flow. For vortex flow, calculate: (a) The time rate of change of the volume of a fluid element per unit volume (b) The vorticity
Your companys largest supplier has just notified you that it is changing its credit and payment terms. Previously, its standard terms were n/30 and the company had no electronic payment option. Under...
In this simulation, you will be asked to compute various income amounts. Assume a tax rate of 30% and 100,000 shares of common stock outstanding during the year. Prepare responses to all parts....
The T. P. Jarmon Company manufactures and sells a line of exclusive sportswear. The firms sales were $600,000 for the year just ended, and its total assets exceeded $400,000. The company was started...
10-13 THANK YOU Exercise 10-13 (Algo) Special offer pricing LO P7 Farrow Company reports the following annual results. The company receives a special offer for 48,000 units at $12 per unit. The...
Find the stationary values (and their classification) of (a) x 15x - 20y + 5 (b) 2x-xy - y (c) 2x + y + 3xy - 3y - 5x + 2 (d) x + y-3(x + y) + 1 (e) xy 2xy - 2x - 3x (f) xy(1-x-y) 2 2 (g) x + y + + x...
Find the value of the constant l such that is the exact differential of a function f(x, y). Find the corresponding function f(x, y) that also satisfies the condition f(0, 1) = 0. (ycosx + Acos y)dx +...
Denver is 1350 km east and 900 km south of Seattle. Edmonton is 620 km east and 640 km north of Seattle. How far is Denver from Edmonton?
Research the control system used by your corporation and select pieces of evidence of informational and behavioral control. Be aware that the evidence must respond to the full definition of each type...
What strategies can organizations employ to effectively manage workforce diversity and foster inclusion to leverage the full potential of their human capital in a globalized marketplace ?
You are given an array of integers representing the prices of a stock on different days. Write a function in JavaScript to calculate the maximum profit that can be obtained by buying and selling the...
The following selected information is available for the payroll computations of a company for the month of November 2021: Name of the Employee Gross Payroll for the month Elvira Robles Gloria...
Enter the code (from the Code tab) into your compiler. Compile your code and run it. Answer the following critical thinking questions. Save your answers in a Word document. What happens if you enter...
A foundation invests $50,000 at simple interest, part at 7%, twice that amount at 4%, and the rest at 5.5%. What is the most that the foundation can invest at 4% and be guaranteed $2660 in interest...
On the basis of the details of the following fixed asset account, indicate the items to be reported on the statement of cashflows: ACCOUNT Land ACCOUNT NO. Balance Date Item Debit Credit Debit Credit...
The hook is subjected to the force of 80 lb. Determine the state of stress at point A at section aa. The cross section is circular and has a diameter of 0.5 in. Use the curved-beam formula to...
The 3/4-in.-diameter shaft is subjected to the loading shown. Determine the stress components at point B. Sketch the results on a volume element located at this point. The journal bearing at C can...
The 3/4-in.-diameter shaft is subjected to the loading shown. Determine the stress components at point A. Sketch the results on a volume element located at this point. The journal bearing at C can...
Port Ormond Carpet Company manufactures carpets. Fiber is placed in process in the Spinning Department, where it is spun into yarn. The output of the Spinning Department is transferred to the Tufting...
Oct. 31: Paid salaries, $45,000 ( 75% selling, 25% administrtive). Data table Data table them to retail stores. The company has three inventory items: and floor lamps. RLC uses a perpetual inventory...
question 1- You borrow a simple loan of SR 500,000, interest rate is 20%, it matures in one year. what's the yied to maturity? question 2- calculate_i for One-Year Discount Bond with price(p) =...

Show that the differential is not exact, but that a constant m can be chosen so that

Question:

g(x, y) = (10x + 6xy + 6y)dx +(9x + 4xy + 15y) dy

Step by Step Answer:

P102 6xy 6y Q9x4xy 152 SO and 6x12y 18x 4y ag and Pdx Qdy is ...View the full answer

Modern Engineering Mathematics

Students also viewed these Sciences questions