Show that the function g(x) = [H(x – a) – H(x – b)] f(x), a

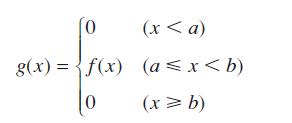
In other words, g(x) is a function that is identical to the function f(x) in the interval [a, b] and zero elsewhere. Hence express as simply as possible in terms of Heaviside functions the function defined by

Transcribed Image Text:

0 g(x)=f(x) 0 (x < a) (ax b) (x = b)