Derive the commutator $left[Q_{i}, Q_{j} ight]=i epsilon_{i j k} Q_{k}$ for the charge defined in Eq. (33.4).
Question:
Derive the commutator $\left[Q_{i}, Q_{j}\right]=i \epsilon_{i j k} Q_{k}$ for the charge defined in Eq. (33.4). Use the charge (33.4) to write the commutator, displaying explicit matrix indices
\[\left[Q_{a}(t), Q_{b}(t)\right]=\int d^{3} x d^{3} x^{\prime} t_{i j}^{a} t_{k l}^{b}\left[q_{i}^{\dagger}(x) q_{j}(x), q_{k}^{\dagger}\left(x^{\prime}\right) q_{l}\left(x^{\prime}\right)\right]\]
where $t^{c} \equiv \frac{1}{2} \tau^{c}$. Then use that the fermion operators anticommute.
Data from Eq. 33.4
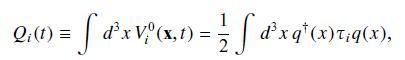
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





