Simpsons rule for the numerical evaluation of an integral is where n is an even number. The
Question:
Simpson’s rule for the numerical evaluation of an integral is
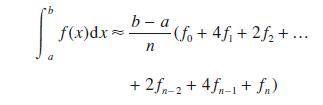
where n is an even number. The global truncation error is
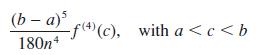
If f(x) = ln cosh x and a = 0, b = 0.5, show that |f(4)(x)| 4). If f(x) is tabulated to 4dp, show that the accumulated rounding error using the formula is less than 1/40 000, and find n such that, using the formula, the integral ∫00.5 ln cosh x dx would be evaluated correctly to 4d
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





