The management of resources often requires a chain of decisions similar to that described in Question 87. Consider the harvesting policy for a large forest. The profit produced from the sale of felled timber is proportional to the square root of the volume sold, while the volume of standing timber increases in proportion to itself year on year. Use the technique outlined in Question 87 to produce a 10-year harvesting programme for a forest.

Data from Question 87

Cross-current extraction methods are used in many chemical processes. Solute is extracted from a stream of solvent by repeated washings with water. The solvent stream is passed consecutively through a sequence of extractors, in each of which a crosscurrent of wash water, flowing at a determined rate, carries out some of the solute. The aim is to choose the individual wash flowrates in such a way as to extract as much solute as possible by the end, the total flow of wash water being fixed.

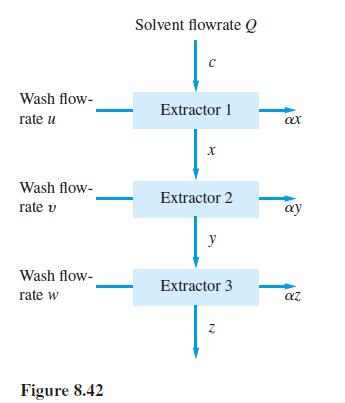
Consider the three-state extractor process shown in Figure 8.42, where c, x, y and z are the solute concentrations in the main stream, and ax, ay and az are the solute concentrations in the effluent wash-water streams, with α a constant. The solute balance equations for the extractors are

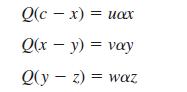
The total wash-water flowrate is W, so that u + v + w = W.

We wish to find u, v and w such that the outflow concentration z is minimized. This is an example of dynamic programming. The key to its solution is the Principle of Optimality, which states that an optimal programme has the property that, whatever the initial state and decisions, the remaining decisions must constitute an optimal policy with respect to the state resulting from the initial decision. This means we solve the problem first for a one-extractor process, then for a two-extractor process, then for a three-extractor process, and so on. For a one-stage process, x is minimized when

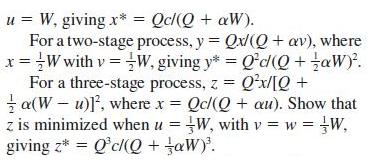
Generalize your answers to the case where n extractors are used.

Transcribed Image Text:

Q(c-x) = uax Q(x - y) = vay Q(y - z) = waz