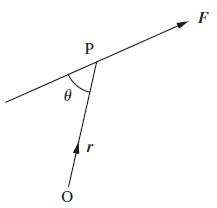
The moment of a force F acting at a point P about a point O is defined to be a vector M perpendicular to the plane containing F and the point O such that |M|= p|F|, where p is the perpendicular distance from O to the line of action of r. Figure 4.44 illustrates such a force F. Show that the perpendicular distance from O to the line of action of F is |r| sin θ, where r is the position vector of P. Hence deduce that M = r × F. Show that the moment of F about O is the same for any point P on the line of action of F. Forces (1, 0, 0), (1, 2, 0) and (1, 2, 3) act through the points (1, 1, 1), (0, 1, 1) and (0, 0, 1) respectively:

(a) Find the moment of each force about the origin.

(b) Find the moment of each force about the point (1, 1, 1).

(c) Find the total moment of the three forces about the point (1, 1, 1).

Figure 4.44