Sometimes an investigator wishes to decide whether a group of m predictors (m > 1) can simultaneously be eliminated from the model. The null hypothesis says that all β’s associated with these m predictors are 0, which is interpreted to mean that as long as the other k − m predictors are retained in the model, the m predictors under consideration collectively provide no useful information about y. The test is carried out by first fitting the “full” model with all k predictors to obtain SSE(full) and then fitting the “reduced” model consisting just of the k − m predictors not being considered for deletion to obtain SSE(red). The test statistic is

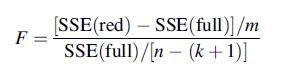
The test is upper-tailed and based on m numerator df and n − (k + 1) denominator df. This procedure is called the partial F test. Refer back to Example 12.26. The following are the SSEs and numbers of predictors for the first-order, complete second-order, and the researchers’ final model.

Data From Example 12.26

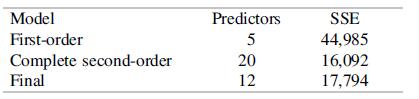
a. Use the partial F test to compare the first-order and complete second-order models. Is there evidence that at least some of the second-order terms should be retained?
b. Use the partial F test to compare the final model to the complete second order model. Do you agree with the researchers’ decision to eliminate the “other” eight predictors?

Transcribed Image Text:

F = [SSE (red) -SSE (full)]/m SSE(full)/[n (k+1)] -