Demonstrate that the Bogoliubov quasiparticle creation and annihilation operators obey the anticommutators (left{alpha_{k}, alpha_{k^{prime}} ight}=left{alpha_{k}^{dagger}, alpha_{k^{prime}}^{dagger} ight}=0)
Question:
Demonstrate that the Bogoliubov quasiparticle creation and annihilation operators obey the anticommutators \(\left\{\alpha_{k}, \alpha_{k^{\prime}}\right\}=\left\{\alpha_{k}^{\dagger}, \alpha_{k^{\prime}}^{\dagger}\right\}=0\) and \(\left\{\alpha_{k}, \alpha_{k^{\prime}}^{\dagger}\right\}=\delta_{k k^{\prime}}\) given in Eq. (22.30), if the bare fermion operators satisfy the
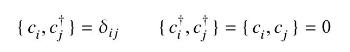
fermionic anticommutator algebra.
Data from Eq. 22.30
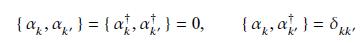
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





