Show that the mean square deviation of the particle number from the actual particle number for a BCS wavefunction is given by

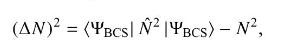
where \(\hat{N}\) is the particle number operator and \(N=\langle\hat{N}angle\) is the average particle number. In quantum mechanics the spread in a distribution of measurements with respect to the average or expectation value is given by the standard deviation \(\sigma\), with

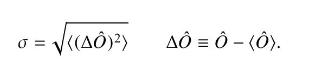
Use this to prove the general result that \(\sigma^{2}=\left\langle\hat{O}^{2}\rightangle-O^{2}\), and then specialize to particle number in the BCS approximation.

Transcribed Image Text:

(AN) (BCS N | YBCS) - N, =