For an operator \(A=a_{\mu} X_{\mu}\) corresponding to a linear combination of generators \(X_{\mu}\) for a Lie algebra, use Eq. (7.10) and the Jacobi identity (3.6) to prove that

\[\left[A,\left[E_{\alpha}, E_{\beta}\right]\right]=(\alpha+\beta)\left[E_{\alpha}, E_{\beta}\right],\]

where \(E_{\alpha}\) and \(E_{\beta}\) are generators that are not in the Cartan subalgebra.

Data from Eq. 7.10

Data from Eq. 3.6

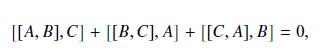
[A, Ea] = E,