For orbital angular momentum $L$, spin angular momentum $S$, total angular momentum $J$, and projection $M$ of the total angular momentum, use the Wigner-Eckart theorem to express $\left\langle L S J M\left|L_{z}+2 S_{z}\right| L S J M\rightangle$ in terms of reduced matrix elements. Evaluate the reduced matrix elements to show that $\left\langle L S J M\left|L_{z}+2 S_{z}\right| L S J M\rightangle=M g$, where the Landé $g$-factor is

\[g \equiv 1+\frac{J(J+1)+S(S+1)-L(L+1)}{2 J(J+1)} .\]

Consult Example 6.9, and note that $L$ operates only on the orbital part and $S$ only on the spin part of the wavefunction, so Eq. (30.12) is appropriate. 

Data from Example 6.9

Data from Eq. 30.12

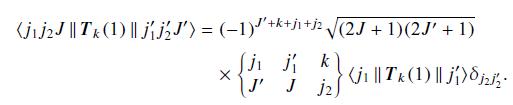
Example 6.9 We first evaluate the reduced matrix elements of the angular momentum operator J, which is a spherical tensor of rank one. Choosing the generator J to be diagonal and also invoking Eq. (6.71) gives two relations, (JM| J | J'M')= M8JJMM' (JM| J |J'M') = (J'M' 10| JM) (J || J || J'), and setting these equations equal gives (J || J || J') = (J' M' 10| JM) MJJM'.