From Problems 2.9 and 2.11, the group D₂= {e, a, b, c} has a factor (quotient) group with respect to the abelian invariant subgroup \(H=\{e, a\}\),

\[\mathrm{D}_{2} / H=H+M=\{e, a\}+\{b, c\}\]

with a map \(\phi\) from \(\mathrm{D}_{2}\) to \(\mathrm{D}_{2} / H\) given by

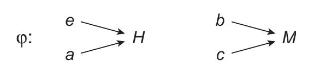
Show that if the space for \(\mathrm{D}_{2}\) is equipped with a topology defined by the open sets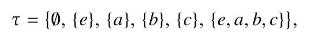the inverse map \(\phi^{-1}\) implies that the quotient space has a topology also.

Data from Problem 2.9

Data from Problem 2.11

Q: e a H b C M