Poincar invariance requires that the action of a scalar field be unchanged under an infinitesimal spacetime translation

Poincaré invariance requires that the action of a scalar field be unchanged under an infinitesimal spacetime translation \(x_{\mu} \rightarrow x_{\mu}^{\prime}=x_{\mu}+a_{\mu}\). Show that this requirement implies the conservation law

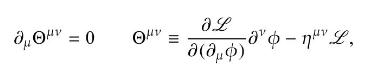
where \(\Theta^{\mu v}\) is a conserved Noether tensor, \(\eta^{\mu v}\) is the metric tensor, and \(\mathscr{L}\) is the Lagrangian density for the scalar field. Show that the components \(\Theta^{00}\) and \(\Theta^{0 k}\) with \(k=1,2,3\) may be interpreted as the energy and momentum densities, respectively, and that generally \(\partial_{\mu} \Theta^{\mu v}=0\) is a statement of 4-momentum conservation.

Transcribed Image Text:

O.L = 0 ) -2 - 2,