Prove that the generators (left(tau_{1}, tau_{2}, K ight)) of Eq. (19.17) for the local (mathrm{SU}(2)_{mathrm{w}} times mathrm{U}(1)_{y})
Question:
Prove that the generators \(\left(\tau_{1}, \tau_{2}, K\right)\) of Eq. (19.17) for the local \(\mathrm{SU}(2)_{\mathrm{w}} \times \mathrm{U}(1)_{y}\) standard electroweak symmetry annihilate the vacuum state but that the charge generator \(Q\) does not.
Data from Eq. 19.17
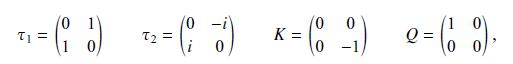
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





