Prove the trigonometric identities by the following group-theoretical means. 1. Show that the complex numbers of unit
Question:
Prove the trigonometric identities
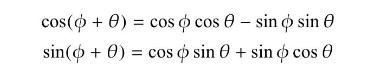
by the following group-theoretical means.
1. Show that the complex numbers of unit modulus \(c=x+i y\) with \(|x|^{2}+|y|^{2}=1\) form a group under multiplication, and that \(e^{i \phi}\) with \(-\pi \leq \phi \leq \pi\) is a faithful representation: \(\cos \phi+i \sin \phi=e^{i \phi}\).
2. Use the representation \(e^{i \phi}\) and group multiplication to prove the identities.
This is a simple example of a more general idea: the special functions of mathematical physics often are representations of some group, and standard identities can be obtained by appropriate operations on the representations of that group.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





