Show that the current (boldsymbol{j}) in Eq. (18.17) is invariant under the gauge transformation (boldsymbol{A} ightarrow
Question:
Show that the current \(\boldsymbol{j}\) in Eq. (18.17) is invariant under the gauge transformation \(\boldsymbol{A} \rightarrow \boldsymbol{A}+\boldsymbol{abla} \chi \equiv \boldsymbol{A}^{\prime}\) and \(\theta \rightarrow \theta+q \chi \equiv \theta^{\prime}\), where \(\chi=\chi(x)\) is an arbitrary scalar function. Assume the static limit (no time dependence) and work in the Coulomb gauge (14.12). Show that a general solution of the atomic screening-current problem requires solution of the coupled equations
\[abla^{2} \boldsymbol{A}=-\boldsymbol{j} \quad-\frac{1}{2 m}(\boldsymbol{abla}-q \boldsymbol{A})^{2} \psi=E \psi\]
where the first equation describes the electromagnetic field and the second describes the motion of the electrons.
Data from Eq. 18.17
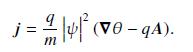
Data from Eq. 14.12
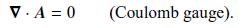
Step by Step Answer:

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun





