Show that the set of matrices ({a, b, c, d}) given by closes under multiplication and is
Question:
Show that the set of matrices \(\{a, b, c, d\}\) given by
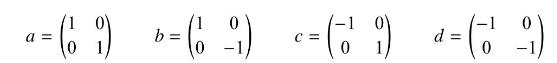
closes under multiplication and is a representation of the group \(\mathrm{D}_{2}\) in Problem 2.9 .
Data from Problem 2.9
Show that the group {e, a, b, c\} with multiplication table (b) below, is in one to one correspondence with the geometrical symmetry operations on figure (a) below

This is called the 4-group or dihedral group \(\mathrm{D}_{2}\). Show that \(\mathrm{D}_{2}\) has three subgroups, \(\{e, a\},\{e, b\}\), and \(\{e, c\}\), each isomorphic to the cyclic group \(\mathrm{C}_{2}\).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Symmetry Broken Symmetry And Topology In Modern Physics A First Course
ISBN: 9781316518618
1st Edition
Authors: Mike Guidry, Yang Sun
Question Posted:





