The Lie bracket of vector fields \(A\) and \(B\) is defined as their commutator, \([A, B]=\) \(A B-B A\). The Lie bracket of two basis vectors vanishes for a coordinate basis but not for a non-coordinate basis. For the 2D plane parameterized with cartesian \((x, y)\) or polar \((r, \theta)\) coordinates and the bases

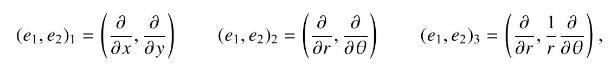
show that \(\left(e_{1}, e_{2}\right)_{1}\) and \(\left(e_{1}, e_{2}\right)_{2}\) are coordinate bases, but that \(\left(e_{1}, e_{2}\right)_{3}\) is not.

(e1, e2)1 1 = (3x-8) a a a a 212 = (8780) (1,2) = (0180) (e1, e2)2 e2)3