Consider a particle in one dimension moving under the influence of some timeindependent potential. The energy levels and the corresponding eigenfunctions for this problem are assumed to be known . We now subject the particle to a traveling pulse represented by a time-dependent potential,

(a) Suppose that at t = -∞ the particle is known to be in the ground state whose energy eigenfunction is

Obtain the probability for finding the system in some excited state with energy eigenfunction ⟨x | f⟩ = u_f(x) at t = + ∞.

(b) Interpret your result in (a) physically by regarding the δ-function pulse as a superposition of harmonic perturbations; recall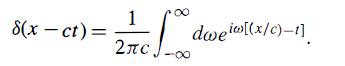

Emphasize the role played by energy conservation, which holds even quantummechanically as long as the perturbation has been on for a very long time.

V(t) = A8(x-ct).