Consider a spinless particle in a two-dimensional infinite square well: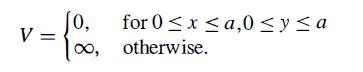

(a) What are the energy eigenvalues for the three lowest states? Is there any degeneracy?

(b) We now add a potential

Taking this as a weak perturbation, answer the following:

(i) Is the energy shift due to the perturbation linear or quadratic in λ for each of the three states?

(ii) Obtain expressions for the energy shifts of the three lowest states accurate to order λ. (You need not evaluate integrals that may appear.)

(iii) Draw an energy diagram with and without the perturbation for the three energy states. Make sure to specify which unperturbed state is connected to which perturbed state.

V [0, for 0x a,0 y a , otherwise.