A large literature, briefly discussed in section 11.4.1, examines the conditions under which agents with incorrect beliefs about fundamentals will be driven out of the market by rational agents in the long run. In this exercise we explore in a partialequilibrium setting some forces that influence the long-run survival of agents with incorrect beliefs.

Consider two agents A and B with wealth levels \(W_{t}^{A}\) and \(W_{t}^{B}\), respectively, who invest in two assets in perfectly elastic supply, a risky asset with \(\log\) return \(r_{t+1}\) and a riskless asset with riskfree rate \(r_{f, t+1}\). The returns to the two assets are iid over time, \(r_{t+1} \sim \mathcal{N}\left(\mu, \sigma^{2}ight)\) and \(r_{f, t+1}=r_{f}\) for all \(t\). The two investors have heterogeneous beliefs about the mean of \(\log\) returns; in particular, they perceive \(r_{t+1} \sim^{i} \mathcal{N}\left(\mu^{i}, \sigma^{2}ight)\), where \(\mu^{i}\) may be different from the true mean \(\mu\). The agents have common Epstein-Zin preferences given by equation (6.34) and no outside income.

Investor A is said to become extinct (relative to investor B) if \(\lim _{t ightarrow \infty} W_{t}^{A} / W_{t}^{B} ightarrow 0\) with probability 1 and is said to survive in the long run otherwise (and similarly for investor B). Long-run survival depends on the logarithmic growth rates of agents' wealth, consistent with the discussions of sections 2.1.5 and 10.3.2; in particular, in this iid setting it can be shown that investor \(A\) survives if and only if \(\mathrm{E}\left[\log \left(W_{t+1}^{A} / W_{t}^{A}ight)ight] \geq\) \(\mathrm{E}\left[\log \left(W_{t+1}^{B} / W_{t}^{B}ight)ight]\).

(a) Argue that the geometric average growth rate of investor \(i\) s wealth, \(i=\{A, B\}\), is given by

where \(w_{t+1}^{i}=\log W_{t+1}^{i}, r_{p, t+1}^{i}\) is the \(\log\) return to investor \(i\) 's financial portfolio, and \(c w^{i}\) is his consumption-wealth ratio.

(b) Using the portfolio approximation (2.24), show that

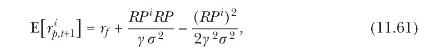
Equation 2.24

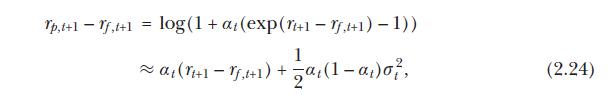
where \(R P=\mu-r_{f}+\sigma^{2} / 2\) and \(R P^{i}=\mu^{i}-r_{f}+\sigma^{2} / 2\). Explain the intuition behind the second and third terms in this expression.
Suppose that \(B\) is rational \(\left(\mu^{B}=\muight)\) but \(A\) is not. Under what conditions will \(A\) choose a portfolio with higher mean \(\log\) return than \(B\) ?

(c) Show that agent \(i\) 's consumption-wealth ratio satisfies

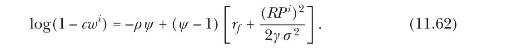
How do subjective beliefs influence the agent's saving rate?
Hint: To derive the expression, use the envelope theorem and equation (6.34) under the conjecture \(U_{t}=v W_{t}\), for some constant \(v\).

Equation 6.34

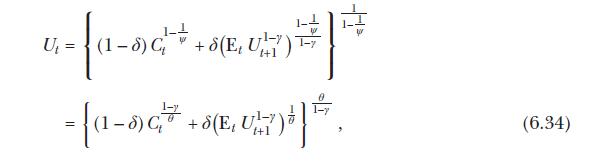
(d) Prove that agent \(i\) will survive if and only if he has the (weakly) lower survival index \(I^{i}\), given by

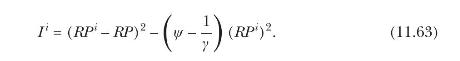
Conclude that under common power utility preferences an irrational agent cannot survive in the presence of a rational agent. Explain why this conclusion can be overturned for general Epstein-Zin preferences.

(e) How would these conclusions change if we allowed for arbitrary heterogeneity in preferences? Based on the preceding analysis, assess the theoretical robustness of the market selection hypothesis, according to which irrational investors will eventually be driven out of financial markets by the rational ones.

Data from section 11.4.1

Data from section 2.1.5

Data from section 10.3.2

Transcribed Image Text:

E[ww]E[+]+log (1-cw'), (11.60)