Consider the following two-factor essentially affine term structure model,

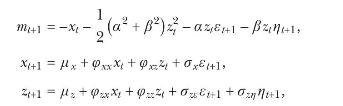
where \(\varepsilon_{t+1}\) and \(\eta_{t+1}\) are independent standard normal variables. Assume \(\sigma_{x}, \sigma_{z \varepsilon}, \sigma_{z \eta}>0\) and that \(x_{t+1}\) and \(z_{t+1}\) are stationary processes.

(a) Why do we call such a model "essentially affine"? Calculate the short rate, \(y_{1 t}\), and the conditional variance of the log SDF, \(\operatorname{var}_{t}\left(m_{t+1}ight)\). Explain that \(z_{t}\) can be interpreted as the price of aggregate market risk. Does the expectations hypothesis hold in this model?

(b) Conjecture that log bond prices are affine in the state variables,

Equation 8.108

Derive the law of motion of the state variables under the risk-neutral measure \(Q\) that prices bonds (the equivalent martingale measure).

(c) Explain intuitively why factor \(z_{t}\) is hidden from (unspanned by) the current term structure if and only if it does not affect the dynamics of \(x_{t}\) under the risk-neutral measure. What is the restriction on the parameters of equations (8.105)-(8.107) such that factor \(z_{t}\) is hidden from the term structure? Is it possible that the current term structure can help forecast future values of \(z_{t}\) if \(z_{t}\) is hidden?
For the rest of this problem, assume that \(z_{t}\) is hidden.

(d) Use the recursive pricing equation for bonds (8.29) to solve for the coefficients in the price function (8.108).

Equation 8.29

(e) Calculate excess returns, \(r_{n, t+1}-r_{1, t+1}\). Show that the conditional term premium, \(\mathrm{E}_{t}\left[r_{n, t+1}-r_{1, t+1}ight]+(1 / 2) \operatorname{Var}_{t}\left(r_{n, t+1}ight)\), is proportional to \(z_{t}\). Interpret the terms in the expression for the term premium and their signs. Why do \(\sigma_{z \varepsilon}\) and \(\sigma_{z \eta}\) not affect the term premia? Finally, explain the intuition for the parameter restriction you derived in part (c).

Transcribed Image Text:

- 22(a + 1 + )-aze-Baner, m+1=-X- X+1= x+Qxxx + 9x + x(+1 2+1 = + xX+0=+0 +1 + Onnt+1>