Consider the risky term structure model of Lettau and Wachter (LW 2007), given by equations (9.53)-(9.56). The model is closely related to the class of essentially affine term structure models with homoskedastic bond yields studied in section 8.3.3. Let \(\sigma_{d z} \equiv\) \(\operatorname{Cov}_{t}\left(d_{t+1}, z_{t+1}ight)\) and denote other covariances similarly.

Equation 9.53

Equation 9.54

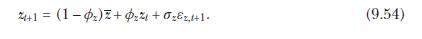
Equation 9.55

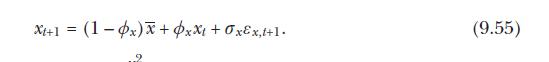
Equation 9.56

(a) The prices of dividend strips (zero-coupon equity) \(V_{n t}\) follow the same recursion as bond prices \(P_{n t}\), (8.29) but subject to a different terminal condition, \(V_{0 t}=D_{t}\) instead of \(P_{0 t}=1\). Conjecture that the log price-to-current-dividend ratio of dividend strips is affine in the state variables:

Equation 8.29

the analogue of (8.58). Derive the recursive equations defining the price coefficients \(A_{n}, B_{x, n}\), and \(B_{z, n}\).

Equation 8.58

(b) Solve for the risk premium, \(\mathrm{E}_{t}\left[r_{n, t+1}ight]-r_{f}+\sigma_{n}^{2} / 2\), and volatility of \(\log\) returns, \(\sigma_{n}^{2}\), on zero-coupon equity as a function of the price coefficients.

(c) Suppose that the price of risk and expected dividend growth have zero contemporaneous covariance with one-period-ahead dividend growth, \(\sigma_{d x}=\sigma_{d z}=0\). Are the term structures of risk premia and Sharpe ratios for zero-coupon equity upward sloping, flat, or downward sloping? Explain.

(d) LW obtain lower risk premia for long-horizon equity than short-horizon equity by assuming that the price of risk is contemporaneously uncorrelated with one-periodahead dividend growth and that dividend growth follows a mean-reverting process, \(\sigma_{d z}

Data from section 8.3.3

Transcribed Image Text:

(896) +1+P3P0+=1+pV