In a market for an individual stock, a fraction \(\mu\) of investors are subject to the disposition effect while the remaining investors are rational. The number of shares demanded by the rational investors takes the linear form:

where \(F_{t}\) is the stock's fundamental value and \(P_{t}\) is its price. The number of shares demanded by the disposition-effect investors is:

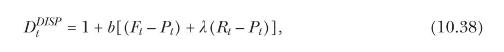
where \(R_{t}\) is a reference price and \(\lambda\) is positive. The disposition effect as formalized in (10.38) reduces demand for "winners" whose price is above the reference price and increases demand for "losers" whose price is below the reference price.

Equation 10.38

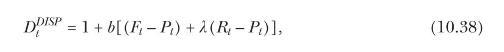
(a) Assume that the supply of the stock is fixed at one unit. Equate supply and demand to show that the equilibrium price must satisfy

for a fixed parameter \(w\). Show that \(w\) does not depend on \(b\), and provide intuition for this result. Write a formula relating \(w\) to \(\mu\) and \(\lambda\), and again provide intuition.

(b) Now assume that fundamental value follows a random walk:

while the reference price adjusts gradually to the actual price:

How might the parameter \(v\) be related to the trading volume in the stock given that microeconomic studies show that an individual investor's purchase price appears to act as a reference price for the investor?

(c) Derive an expression relating the change in the stock price to current and lagged innovations in fundamental value \(\varepsilon_{t+1}\). Show that lagged innovations have a positive effect on price changes whenever \(w\) is less than one. Discuss the effect of \(v\) on price dynamics. What testable implications does this model have relative to other possible explanations for momentum in stock returns?

Transcribed Image Text:

DRAT = 1+ b(F-P), (10.37)