Orlandi and Carnevale [37] argue that the nonlinear amplification of vorticity in inviscid interaction is a candidate
Question:
Orlandi and Carnevale [37] argue that the nonlinear amplification of vorticity in inviscid interaction is a candidate for the appearance of a finite-time singularity of the second kind starting from smooth initial data, check Eq. (3.15) in Chap. 3 for definition. The ode
\[ \frac{\partial \Phi}{\partial t}=\Phi^{2} \]
with initial condition \(\Phi(0)>0\) is a simplified version of the vorticity pde. It has a finite-time singularity developing from positive initial data. Prove this.
Eq. (3.15)
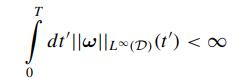
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann
Question Posted:





