Solve the Hopf fde for the Burgers pde using the solution operator established in Problem (9.2). The
Question:
Solve the Hopf fde for the Burgers pde using the solution operator established in Problem (9.2). The initial condition is the characteristic functional \(\theta[y ; 0]\) for Gaussian stochastic fields with zero mean.
9.3.1: Specify the initial condition for Gaussian random fields in terms of the covariance function \(R\left(x, x^{\prime}\right) \equiv\left\langle u(0, x) u\left(0, x^{\prime}\right)\rightangle\) and zero mean. Assume that the covariance function is a function of \(\left|x-x^{\prime}\right|\) and work out the special case \(R\left(x, x^{\prime}\right)=\) \(\sigma_{0}^{2} \delta\left(x-x^{\prime}\right), \sigma_{0}>0\left(R\left(x, x^{\prime}\right)\right.\) is delta correlated \()\).
9.3.2: Construct a basis in \(L_{\mathcal{D}}^{2}\) using Hermite functions (physicists version) \(\Psi_{n}(x)\) (4.29) as defined in (4.30).
9.3.3: Adapt the initial condition to the Hermite basis.
9.3.4: Adapt the fde obtained in Problem (9.2) to the basis constructed.
9.3.5: Solve the fde (9.2) using the relation (6.3) for the measure \(\mu\) at times zero and \(t>0\) assuming that the solution operator generates a bijective map of \(l^{2}\), isomorphic to \(L_{\mathcal{D}}^{2}\), onto itself.
Problem 9.2
Derive the Hopf fde for the characteristic functional \(\theta[y ; t]\) for the pure IVP of the Burgers pde (1.2). Use the result obtained in Problem (9.1) to establish the solution operator and its inverse.
Problem 9.1
Solve the pure IVP for the Burgers pde (1.2) with initial condition \(u(0, x)=u_{0}(x) \in L_{\mathcal{D}}^{2} \cap C_{\mathcal{D}}^{\infty}, \mathcal{D}=(-\infty, \infty)\), using the Hopf-Cole transformation (1.3).
Pde (1.2)

Eq (1.3)
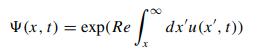
Eq (4.29)

Eq (4.30)
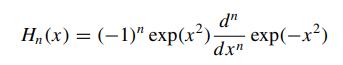
Eq (6.3)
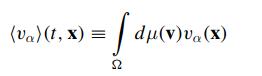
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann





