Derive the Hopf fde for the characteristic functional (theta[y ; t]) for the pure IVP of the
Question:
Derive the Hopf fde for the characteristic functional \(\theta[y ; t]\) for the pure IVP of the Burgers pde (1.2). Use the result obtained in Problem (9.1) to establish the solution operator and its inverse.
Problem 9.1
Solve the pure IVP for the Burgers pde (1.2) with initial condition \(u(0, x)=u_{0}(x) \in L_{\mathcal{D}}^{2} \cap C_{\mathcal{D}}^{\infty}, \mathcal{D}=(-\infty, \infty)\), using the Hopf-Cole transformation (1.3).
Pde (1.2)

Eq (1.3)
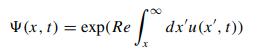
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann
Question Posted:





