12.2 Consider the infant temperament study data of Rubin and Stern (1994), in the form of counts ni jk relating to three behaviour measures of N = 93 infants. These are motor activity at age 4 months (X), with levels i = 1, . . . , 4, and higher categories denoting greater activity; fret/cry activity at 4 months (Y with levels j = 1, 2, 3), and fear level at 14 months (Z with levels k = 1, 2, 3). The data are list(n = structure(.Data = c(5, 4, 1, 0, 1, 2, 2, 0, 2, 15, 4, 2, 2, 3, 1, 4, 4, 2, 3, 3, 4, 0, 2, 3, 1, 1, 7, 2, 1, 2, 0, 1, 3, 0, 3, 3), .Dim = c(4, 3, 3)), I = 4, J = 3, K =3)

Consider latent class models in which X, Y and Z are imperfect measures of an underlying latent variable L, such that within sub-populations defined by L, the observed variables are independent. As mentioned in Section 12.3 one may estimate the model for individuals or use an aggregate approach. This may be done via a loglinear model (see Example 12.2)

or by exploiting the conditional independence result

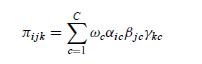
where πi jk = Pr(X = i, Y = j, Z = k) is the joint marginal probability of a positive response on items i, j and k, αic = Pr(X = i |L = c), βjc = Pr(Y = j |L = c), and γkc = Pr(Z = k|L = c). Then (n111, . . . , n433) ∼ Mult(N, [π111, . . . , π433].
The option C = 1 is equivalent to conventional independent factors log-linear model, while Rubin and Stern (1994) cite substantive basis for a two class model (C = 2)
distinguishing infants with low motor and fret activity and low fear (class c = 1) from infants with higher motor and fret activity, and also higher fear (class c = 2). The Dirichlet prior parameters relating toαic, βjc, and γkc used by Rubin and Stern are intended to ensure consistent labelling. Thus they assume αi1 ∼ Dir(0.45, 0.35, 0.15, 0.05),βj1 ∼ Dir(0.8, 0.15, 0.05),γk1 ∼ Dir(0.8, 0.15, 0.05), whereas αi2 ∼ Dir(0.05, 0.15, 0.35, 0.45),βj2 ∼
Dir(0.05, 0.15, 0.8),γk2 ∼ Dir(0.05, 0.15, 0.8) together with a Dirichlet prior Dir(0.55, 0.45) on the latent class mixture probabilities ωc.
One might also apply extra constraint(s) to ensure against label switching with regard to the latent classes. For example if an initial analysis without such constraints suggests clear differentiation in the class probabilities αic (for c = 1 as against c = 2), or in the mixture probabilities ωc, then this differential may be used to set a constraint in a final analysis.
Fit the C = 1 and C = 2 models and use the criterion L2 = 2 i jk ni jklog(ni jk/ˆni jk)
in a posterior predictive check to assess whether the independence and two class models are compatible with the data; this involves sampling new data nnew,i jk at each iteration.
Finally apply the alternative log-linear model approach (e.g. as in Example 12.2) using priors consistent with a unique labelling.

Transcribed Image Text:

ijk wedicjelke