12.3. (Sec. 12.2) U=a'XIl, V=-y'X(2), CU2=1=CV2, where a and -yare vectorS. Show that choosing a and -y
Question:
12.3. (Sec. 12.2)
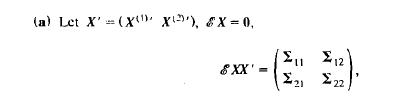
U=a'X\Il, V=-y'X(2), CU2=1=CV2, where a and -yare vectorS.
Show that choosing a and -y to maximize C UV is equivalent to choosing a and -y to minimize the generalized variance of (U V).
lb) Let X' = (X(I)' X(2)' X(3)'), C X = 0,
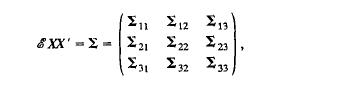
U=a'X(I), V=-y'X(23), W=\3'X(.1), CU 2=CV2=CW2=1. Consider finding
a, -y, \3 to minimize the generalized variance of (U, V, W). Show that this minimum is invariant with respect to transformations X*(i) = AIXU),IAII '" O.
(e) By using such transformations, transform I into the simplest possible form.
(d) In the case of X(I) consisting of two components, reduce the problem (of minimizing the generalized variance) to its simplest form.
le) In this case give the derivative equations.
If) Show that the minimum generalized variance is 1 if and only if 112 = 0, 113 = 0, 123 = O. (Note: This extension of the notion of canonical variates does not lend itself to a "nice" explicit treatment.)
Step by Step Answer:

An Introduction To Multivariate Statistical Analysis
ISBN: 9780471360919
3rd Edition
Authors: Theodore W. Anderson






