4.16. (Sec. 4.2) Let kN(r, p) be the density of the sample corrclation coefficient r for a given value of P and N. Prove that r has a monotone likelihood ratio; that is, show that if PI > P2' then kN(r, PI)/kN(r, P2) is monotonically increasing in r. [Hint: Using (40), prove that if

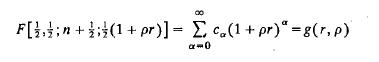
has a monotone ratio, then kN(r, p) does. Show

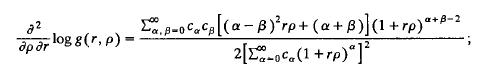
if (B 2/BpBr)Iogg(r, p) > 0, then g(r, p) has a monotone ratio. Show the numerator of the above expression is positive by showing that for each IX the sum on f3 is positive; use the fact that ca + 1

Transcribed Image Text:

Fn+(1+pr)] = ca(1 + pr) = g(r,p) a10