5.15. (Sec. 5.6.2) T 2-test as a Bayes procedure [Kiefer and Schwartz (1965)]. Let XI' ... , X N be independently distributed, each according to N( fl., I). Let TI 0 be defined by [fl.,::£] = [0,([ + TJTJ')-I] with TJ having a density proportional to II+TJTJ'I-~N, and let TIl be defined by [fl.,::£)=[([+TJTJ,)-ITJ,([+TJTJ,)-I]

with TJ having a density proportional to

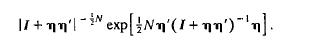
(a) Show that the lleasures are finite for N> p by showing TJ'([ + TJTJ')-ITJ!O 1 and verifying that the integral of II + TJTJ'I- tN = (1 + TJTJ')- tN is finite.

(b) Show that the inequality (26) is equivalent to Ni'(L~_IXaX~)-IX"2!k.
Hence the T2-test is Bayes and thus admissible.

II+ exp[Nm' (I+qm')'n]