6. Consider the SSVS model (George and McCulloch, 1993, 1997) under the prior where j =...
Question:
6. Consider the SSVS model (George and McCulloch, 1993, 1997) under the prior
![]()
where δ j = 1 corresponds to including X j , and {c2j , τ 2 j } are chosen so that δ j = 0 means that effectively βj = 0, whereas c2j τ 2 j is large and permits search for non-zero βj . Assume a preset prior probability pj = Pr(δ j = 1). Then with y = Xβ + ε, where X[n × p] includes an intercept, and ε ∼ N(0, σ2), the prior on β has the form β| ∼ Np(0, DRD), where = (δ1, . . ., δp), R is a prior correlation matrix and D = diag(apτp, . . ., apτp)
where aj = 1 if δ j = 0, and aj = c j if δ j = 1. Assume σ2 ∼ IG(ν, λ) and
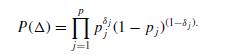
Obtain the joint posterior of β, σ2, and given y, and the conditional posteriors (β|σ2, , y), (σ2|β, , y) and (δ j |β, [ j ], y), where [ j ] = (δ1, . . ., δ j−1, δ j+1, . . . , δp).
Step by Step Answer:







