Consider the equation

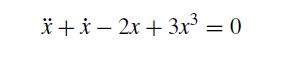
(a) Write a MATLAB program that produces the phase plane. You are welcome to use any integration method you would like. The phase plane portrait that you make should be wide enough to show all of the steady states. Explain why you do (or do not) see the behavior predicted by a linear stability analysis.

(b) This problem gets very interesting if you also include a time-dependent forcing term. Let’s modify the problem to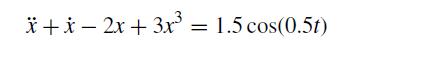

Modify your MATLAB program from part (a) to integrate this modified problem from the initial condition x₀ = −1 and ˙x₀ = 1 out to a very long time – at least up to a total time of t = 10³. Can you explain what is going on here? (It is complicated, but try to explain it.)

Transcribed Image Text:

x + x - 2x + 3x³ = 0