In this problem, we will look at the phase plane dynamics of a particle in a doublewell potential given by the dynamic equation

The term on the left-hand side is the acceleration, and the term on the right-hand side is the force due to a potential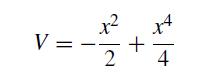

If you plot the potential, you will see that it has a familiar form from physics. This problem is easily converted into a dynamic phase plane by considering the position, x, as the x-axis and the velocity, v = ˙x, as the y-axis.

You should write a MATLAB program that uses a fourth-order Runge–Kutta integration scheme with step size h = 0.01 to integrate the dynamical system. Consider the following initial positions: (x = 1.4142, v = 0) and (x = 1.4143, v = 0). Plot the trajectory for the first position as a blue line and the trajectory for the second position as a red line. To complete at least one cycle, use 10⁴ time steps. Use your knowledge of the phase plane and stability to explain what is happening with these two initial positions that differ only by x = 10⁻⁴. It may be useful for you to zoom your plot to look at where the trajectories begin to diverge but this is not necessary to solve the problem.

Transcribed Image Text:

εX-X = X