In this problem, you are going to look at how the numerical accuracy of the derivative affects the rate of convergence in Newton’s method. Consider the calculation of the root of

with an initial guess x⁽⁰⁾ = 1. In the most accurate case, you would use an analytical calculation of f′(x). However, you can also approximate the derivative using a centeredfinite difference formula,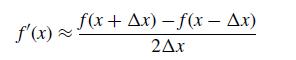

where Δx is the discretization. We will discuss finite differences in much more detail when we cover boundary value problems in Chapter 6. You can think of the analytical case as the limit Δx → 0.

Write a program that implements Newton’s method for values of Δx = 0, 0.01, 0.02, . . ., 0.50 using the initial guess x⁽⁰⁾ = 1. For Δx = 0, you should use the analytical calculation of f′(x) in Newton’s method; for the other cases, you should use the finite-difference approximation. Set your convergence criteria to |f (x^(k))| −6 for iteration k. The error in the derivative can become very severe as you increase Δx, so also add a check in your Newton’s method to stop the iterations if k ≥ 250. You should record the number of iterations and the root x^∗ for each value of Δx. If the scheme does not converge, record a value of zero for the number of iterations and the root. Your program should automatically perform this calculation for Δx = 0, 0.01, 0.02, . . ., 0.50. It should make a plot of the number of iterations k versus Δx, using k = 0 if the solution does not converge. In addition to making a plot, compile your output into a matrix that you can save to file using dlmwrite. The matrix should have 51 rows and the following three columns: (i) Δx, (ii) the value of the root, and (iii) the number of iterations for convergence.

Transcribed Image Text:

f(x) = et² - 2x³ + sin(3x)