For a packed bed, the Ergun equation provides a relationship between the pressure drop per unit length and the properties of the bed,

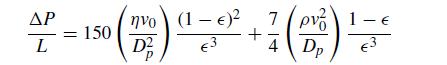
where η is the fluid viscosity, v₀ is the superficial velocity, D_p is the particle diameter, ρ is the fluid density, and ϵ is the void fraction of the bed. Consider a 1.5 m long packed bed containing 5 cm diameter particles. Fluid of density 2 g/cm³ and viscosity 1 cP flows through this bed at a superficial velocity of 0.1 m/s. The pressure drop in the bed is 416 Pa.

(a) Write a program that uses Newton’s method to determine the void fraction of the bed and outputs it to screen along with the number of iterations and the value of |f(x)|. Provide the equations needed for Newton’s method along with evidence from your program that the solution has quadratic convergence. (You should pick a bad initial guess and a very small tolerance to see the quadratic convergence.)

(b) Now let’s use the program from the first part to see how the solution speed is affected by the initial guess. Modify your program from part (a) to compute the number of iterations required for convergence with a tolerance |f (ϵ)| −14 for initial guesses ϵ⁽⁰⁾ = 0.01, 0.02, . . ., 0.99. You program should automatically plot the number of iterations versus the initial guess for ϵ. Does this plot make sense?

L = 150 ) (1 )2 - D3 p + 7 pv 4 \ D, 1-