Consider the partial differential equation subject to the constant concentration boundary condition c(0, t) = 0 and
Question:
Consider the partial differential equation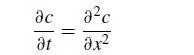
subject to the constant concentration boundary condition c(0, t) = 0 and the reaction–diffusion boundary condition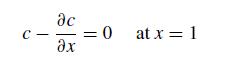
and the initial condition c(x, 0) = 1. The solution to this problem is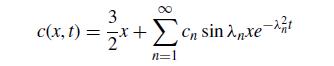
where λn are the positive roots of![]()
the Fourier coefficients for n = 1, 2, . . . are
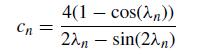
The goal here is to figure out how to make a plot of the concentration profile.
(a) Write a MATLAB program that plots the eigenvalue equation from λ∈ [−10, 10]. This will help you with finding the roots since you can see roughly where the first few positive roots are located. Estimate for λ1 by looking at the graph.
(b) Write a MATLAB program that finds λ1 using Newton’s method using the guess you obtained from part (a). The program should output the value of λ1 to the screen. What is the function f(λ) and the derivative f′(λ) needed for Newton’s method?
(c) Now let’s see if we can find many of the eigenvalues using your program from part(b). In the first part of your program, you should automatically find the first ten positive eigenvalues and print them to screen. To be sure that you got the right values, it may be useful for you to use the program from part (a) to plot the eigenvalue equation and put your results on top of the function as circles. (This is not required, but it is very helpful to make sure that my program works.) In the second part of your program, you should automatically find the first 150 positive eigenvalues and determine how λn+1 − λn depends on the eigenvalue number n. Plot this result and explain the asymptotic value for large n.
(d) Write a MATLAB program that automatically generates a plot of the function c(x, t) for the times t = 0.0005, 0.01, 0.05, 0.07, and 0.2.
Step by Step Answer:

Numerical Methods With Chemical Engineering Applications
ISBN: 9781107135116
1st Edition
Authors: Kevin D. Dorfman, Prodromos Daoutidis




