This problem consists of three numerical calculations that involve the coupled reaction–diffusion system

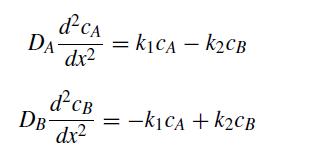
where D_A and D_B are the diffusion coefficients for species A and B, respectively, and k₁ and k₂ are reaction rates. The boundary conditions for these equations are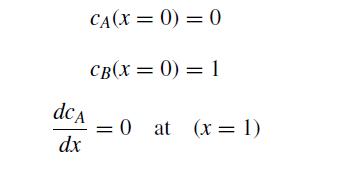

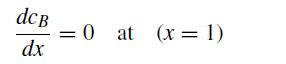
You will write three different programs for this problem, but each one builds on the previous one. It may be helpful to copy-and-paste between programs.

(a) Write a MATLAB program that computes the composition as a function of position using centered finite differences with D_A = 2, D_B = 1, k₁ = 9, and k₂ = 10. What are all of the equations that you will need in the numerical solution? For the numerical solution, use a sparse matrix, especially if you want to use a large number of grid points. Your program should automatically plot the concentrations of A and B as a function of position.

(b) While the concentrations are fixed at the left boundary, the concentrations at the right boundary are harder to predict. In this problem, develop a bracketing method that determines the value of k₂ = k^∗₂ such that c_A(x = 1) = c_B(x = 1) for D_A = D_B = 1 and k₁ = 10. In this bracketing method, you should pick some value of k₂ and use the integration method from part (a) to compute the values of c_A and c_B at the right boundary. If the ratio of concentrations c_A/c_B is not within to 1 ± 10⁻⁶, your program should update the value of k₂ in some intelligent manner until it converges to within the latter tolerance. There are many ways to design this bracketing method, so this is an opportunity for you to demonstrate your creativity in the numerical method. Explain how your bracketing method works and report the value of k2 that gives equal concentrations at x = 1.

(c) Use the programs from the previous two problems to explore how the value of k^∗₂ depends on the diffusion coefficient D_B with D_A = 1 and k₁ = 10. Copying from the programs you have already written, make a new MATLAB file that loops through the values D_B = 0.1, 0.2, . . . , 10 and automatically determines the corresponding value of k^∗₂. Your program should also plot k^∗₂ versus D_B.

Data from Problem 23

Write a MATLAB program that uses finite difference to solve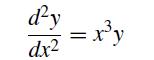

on x ∈ [0, 1] subject to y(0) = 1 and y′(1) = 0 and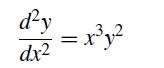

on x ∈ [0, 1] subject to y(0) = 1 and y′(1) = 0. Use the solution to the linear problem, y″ = x3y as the initial guess. Your program should plot the solutions to both the linear and the nonlinear problems on the same graph.

Data from Problem 22

Write a MATLAB program that solves the coupled system of equations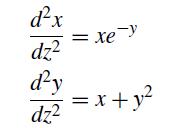

subject to x(1) = 0.8, y(1) = 1, dx/dz = 0 at z = 0, and dy/dz = x at z = 0 using interleaved variables. Your program should generate a plot of x(z) and y(z).

Transcribed Image Text:

d²CA DA dx² d-CB DB- dx² = k1CA - K₂CB -K1CA + K₂CB