This problem deals with the numerical analysis of the solution to This is a separable ordinary differential
Question:
This problem deals with the numerical analysis of the solution to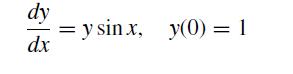
This is a separable ordinary differential equation with the solution![]()
The exact solution is denoted as y∗ for future reference.
(a) We will begin by looking at the solutions produced by using either explicit Euler or RK4 and comparing them to the exact solution over the interval x ∈ [0, 10].Write a MATLAB program that solves the ODE for x = 10−3, 10−2, 10−1, 0.2, 1, and 2. For each value of x, your program should automatically produce a plot of y(x) for the exact result, explicit Euler, and RK4.
(b) Now that we have a working code that (hopefully) produces sensible results, let’s do some analysis of the accuracy of the solution and the time. Modify your program from part (a) so that it determines the error in the solution, which we will define as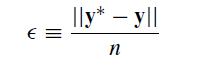
where y is the numerical solution, y∗ is the exact solution evaluate at the same points in x, and n is the number of points in each vector. You should also keep track of the time required for the solution. MATLAB has built in functions for this purpose called tic and toc. The syntax is
This calculation should be done for 50 logarithmically spaced values of x between 10−5 and 1. MATLAB has a function logspace that you may find convenient for this purpose. Note that the integrals will not hit x = 10 exactly, so you can either stop at the point just before x = 10 or just after x = 10. Your program should automatically produce two plots: (i) the values of the error for explicit Euler and RK4 versus Δx, and (ii) the time required or explicit Euler and RK4 versus Δx. Discuss both plots with respect to errors in integration and the amount of work required for these methods.
(c) Let’s now repeat part (b) using implicit Euler and compare the results for the error and the time with explicit Euler. Modify the program from part (b) to also do implicit Euler integration for the same range of Δx and produce the same two plots: (i) the values of the error for explicit and implicit Euler versus Δx, and (ii) the time required or explicit and implicit Euler versus Δx. Explain both the time for the solution and the error that you see in your plots. You may find it useful to make some plots of the solutions for representative values of Δx to help with your explanation. You should also include the details of how you implemented Newton’s method in your implicit solution.
Important suggestion: The calculation of part (c) may take some time for your computer to complete. You should begin with a reasonably large step size, such as Δx = 0.1, to debug the program before you attempt to run all of the calculations. You can use the same idea in parts (a) and (b), but they should run much more quickly so it is less of an issue.
Step by Step Answer:

Numerical Methods With Chemical Engineering Applications
ISBN: 9781107135116
1st Edition
Authors: Kevin D. Dorfman, Prodromos Daoutidis




