This problem involves the analysis of a counter-current heat exchanger. The design equation for a counter-current heat exchanger is

where Q is the heat transferred between streams, A is the area of the exchanger, and the log-mean temperature is defined as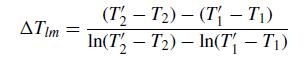

where T₁ is the inlet temperature of the inner stream, T₂ is the outlet temperature of the inner stream, T′₂ is the inlet temperature of the outer stream, and T′₁ is the outlet temperature of the inner stream. The first law of thermodynamics requires that

where m˙ is the flow rate of the inner stream, C_p is the heat capacity of the inner stream, and we have chosen to set T₂ > T₁ so that Q is positive. A similar energy balance applies to the outer stream.

(a) We will begin by reviewing the analysis of a counter-current heat exchanger. The inner fluid has a flow rate of 3 kg/s and a heat capacity of 2.3 kJ/kg°C and the outer fluid has a flow rate of 5 kg/s and a heat capacity of 4 kJ/kg°C. The heat exchanger cools the inner fluid from 100°C to 50°C and the outer fluid enters at 15°C. The overall heat transfer coefficient is 1 kW/m2 °C. Determine the outlet temperature of the cooling fluid and the area of the heat exchanger. Use of MATLAB is not required.

(b) We now want to figure out the outlet temperature of the inner fluid if we change the flow rate of the cooling fluid. Write a MATLAB program that uses Newton’s method to compute this quantity. Test your program using the same parameters as part (a) with an initial guess of 1000°C (which makes no sense physically) and demonstrate quadratic convergence. Include all relevant calculations in your written solution (e.g., the nonlinear equation and its derivative) and include a printout of the data demonstrating quadratic convergence.

(c) Use your Newton’s method algorithm from part (b) to compute the outlet temperature of the inner fluid as a function of the cooling fluid flow rate for logarithmically spaced flow rates from 10^−1/2 to 10³ kg/s. Your program should automatically generate a semilog-x plot of temperature versus cooling flow rate.

Transcribed Image Text:

Q = UAATIm