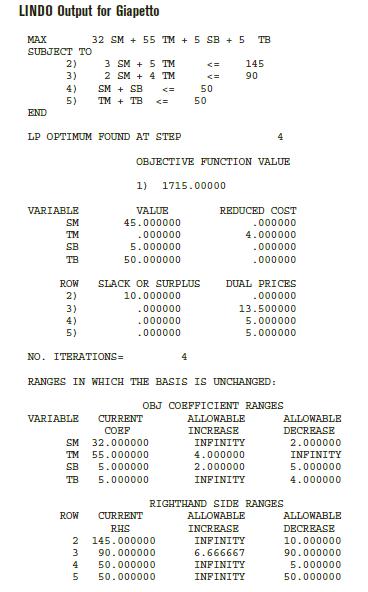
8 Wivco produces two products: 1 and 2. The relevant data are shown in Table 12. Each week, up to 400 units of raw material can be purchased at a cost of $1.50 per unit.

The company employs four workers, who work 40 hours per week. (Their salaries are considered a fixed cost.)

Workers are paid $6 per hour to work overtime. Each week, 320 hours of machine time are available.

In the absence of advertising, 50 units of product 1 and 60 units of product 2 will be demanded each week. Advertising can be used to stimulate demand for each product.
Each dollar spent on advertising product 1 increases its demand by 10 units, and each dollar spent for product 2 increases its demand by 15 units. At most $100 can be spent on advertising. Define P1 = number of units of product 1 produced each week P2 = number of units of product 2 produced each week OT = number of hours of overtime labor used each week RM = number of units of raw materials purchased each week A1 = dollars spent each week on advertising product 1 A2 = dollars spent each week on advertising product 2 Then Wivco should solve the following LP:

All variables non-negative Use LINDO to solve this LP. Then use the computer output to answer the following questions:
a If overtime cost only $4 per hour, would Wivco use it?
b If each unit of product 1 sold for $15.50, would the current basis remain optimal? What would be the new optimal solution?
c What is the most that Wivco should be willing to pay for another unit of raw material?
d How much would Wivco be willing to pay for another hour of machine time?
e If each worker were required (as part of the regular workweek) to work 45 hours per week, what would the company’s profits be?
f Explain why the shadow price of row (1) is 0.10.
(Hint: If the right-hand side of (1) were increased from 50 to 51, then in the absence of advertising for product 1, 51 units of product 1 could now be sold each week.)
9 In this problem, we discuss how shadow prices can be interpreted for blending problems (see Section 3.8). To illustrate the ideas, we discuss Problem 2 of Section 3.8. If we define x6J = pounds of grade 6 oranges in juice x9J = pounds of grade 9 oranges in juice x6B = pounds of grade 6 oranges in bags x9B = pounds of grade 9 oranges in bags then the appropriate formulation is

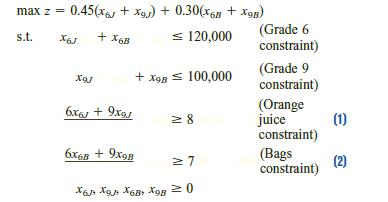
Constraints (1) and (2) are examples of blending constraints because they specify the proportion of grade 6 and grade 9 oranges that must be blended to manufacture orange juice and bags of oranges. It would be useful to determine how a slight change in the standards for orange juice and bags of oranges would affect profit. At the end of this problem, we explain how to use the shadow prices of Constraints (1) and (2) to answer the following questions:
a Suppose that the average grade for orange juice is increased to 8.1. Assuming the current basis remains optimal, by how much would profits change?
b Suppose the average grade requirements for bags of oranges is decreased to 6.9. Assuming the current basis remains optimal, by how much would profits change?
The shadow price for both (1) and (2) is 0.15. The optimal solution to the O.J. problem is x6J 26,666.67, x9J
53,333.33, x6B 93,333.33, x9B 46,666.67. To interpret the shadow prices of blending constraints (1) and (2), we assume that a slight change in the quality standard for a product will not significantly change the quantity of the product that is produced.
Now note that (1) may be written as

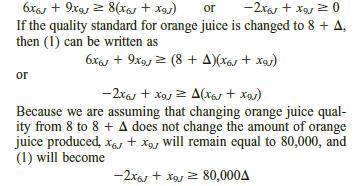
Using the definition of shadow price, answer parts

(a) and (b).

Transcribed Image Text:

LINDO Output for Giapetto 32 SM 55 TM +5 SB + 5 TB MAX SUBJECT TO 2) 3 SM 5 TM