Example 1.6-1 revises the 50-50 guesstimate (prior) probability based on the parking lot observation, yielding a posterior probability which may then be used as prior probability for a succeeding observation. Suppose that the succeeding observation is represented by the statistics given in Problem 1-21. Revise the posterior probability based on the two combined observations (parking lot then ratings) and comment on the effect of the second observation on the decision to find a restaurant that offers good meals.

Example 1.6-1

You arrived in a town and are looking for a good meal before retiring for the night. Not knowing the town, you start with a guesstimate prior probability of 50% chance (event A) that any restaurant will offer a good meal. Next, you surmise from past travel experience that a full parking lot (event B) of a restaurant translates to an 80%-chance that the place offers good meals. Available date estimates that only 55% of the town restaurants have full parking lots. How would this evidence change your initial 50-50 estimate?

The prior probability is P(A) = .5, the likelihood probability P(B|A) = .8, and P(B) = .55. Thus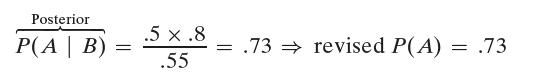

The revised P(A) shows that full parking lots boosts the probability of offering good meals from the initial guesstimate of .5 to the new favorable probability of .73. Other evidence (such as restaurant ratings) can be used to revise new P(A) = .73 to higher or lower values depending on their associated probabilities.

Transcribed Image Text:

Posterior P(A | B) = .5 x .8 .55 = .73 ⇒ revised P(A) = .73