Question: In 1871 Sellmeier derived the equation where the A j terms are constants and each Î» 0j is the vacuum wavelength associated with a natural

In 1871 Sellmeier derived the equation

Ад? r = 1+ ):

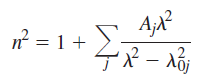
where the A_jterms are constants and each Î»_0j is the vacuum wavelength associated with a natural frequency v_0j, such that Î»_0jv_0j= c. This formulation is a considerable practical improvement over the Cauchy Equation. Show that where Î» > > Î»_0j, Cauchy€™s Equation is an approximation of Sellmeier€™s. Write the above expression with only the first term in the sum; expand it by the binomial theorem; take the square root of n² and expand again.

? r = 1+ ):

Step by Step Solution

★★★★★

3.52 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Binomially expanding n 2 1 A1 2 0 2 givesn 2 1 A... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Optics Questions!

What is the de Broglie wavelength associated with a 1000-kg car moving at 25 m/s?

The hydrogenbromine reaction corresponds to the production of HBr(g) from H 2 (g) and Br 2 (g) as follows: H 2 (g) + Br 2 (g) 2HBr(g). This reaction is famous for its complex rate law, determined by...

What is the wavelength associated with a photon that will induce a transition of an electron spin from parallel to anti-parallel orientation in a magnetic field of magnitude 0.200T? Assume that l = 0.

Question 3 Console outputs that you are required to write your code to exactly match them are written at the very end of the paper. Q4, Q5 and Q6 looks dependent in the code below. However, they will...

Question 2 Console outputs that you are required to write your code to exactly match them are written at the very end of the paper. Q4, Q5 and Q6 looks dependent in the code below. However, they will...

Calculate this financial ratio for the years 2020 with the following ratio categories: 1. Liquidity ratio 2. activity/ efficiency ratio 3. leverage/debt ratio Notes to the Financial Statements - 31...

Please use the following documents to answer: What. are the two kinds of accounting leases that Southwest reports on its balance sheet? Which balance sheet account has changed most noticeably with...

Calculate the financial ratio for the years 2020 and show the calculations in table with the following ratio categories: 1. Liquidity ratio 2. activity/ efficiency ratio 3. leverage/debt ratio...

Bloomberg CASEO Businessweek STUDIES E Financial Statements Analysis Compare financial statement ratios The Financial Statements Analysis case study includes two sep- to identify critical objective...

Jacobson v. Massachusetts, 197 U.S. 11 (1905) Argued: December 6, 1904 Decided: February 20, 1905 Argued: December 5, 1904 Decided: February 19, 1905 Annotation PRIMARY HOLDING A state may enact a...

Zimba Technology Corp. recently went public with an initial public offering of 2.5 million shares of stock. The underwriter used a firm commitment offering in which the net proceeds was $8.05 per...

Find the future value of $10,000 invested now after five years if the annual interest rate is 8 percent. A. What would be the future value if the interest rate is a simple interest rate? B. What...

When evaluating the viability of a project, what does the test of economic efficiency require? Question 6 options: NPV and BCR are greater than or equal to 0 . NPV is greater than 0 or BCR is greater...

Exercise 21.1.1 Derive the formula for the change in the T-bill futures invoice price per tick with 91 days to maturity.

Find the tensions in the ropes illustrated in Fig. 4-4(a) if the supported body weighs 600 N. FTA 70 FTs Fri 30% 30% 600 N (a) 70 F12 B

A 50-N box is slid straight across the floor at constant speed by a force of 25 N, as depicted in Fig. 4-3(a). (a) How large a friction force impedes the motion of the box? (b) How large is the...

A rope extends between two poles. A 90-N boy hangs from it as shown in Fig. 4-2(a). Find the tensions in the two parts of the rope. 10 Fri M (a) 5.0 Fr Fr sin 104 Fr 10 Fricos 10 Fig. 4-2 (b) 5.0 Fr...

Carter Corporation's sales are expected to increase from $5 million in 2012 to $6 million in 2015, or by 20%. Its assets totaled $2 million at the end of 2014. Carter is at full capacity, so its...

A Japanese exporter has a 61,000,000 receivable due in one year. Detail a strategy using a money market hedge that will eliminate any exchange rate risk. 1-year rates of interest Spot exchange rates...

Investment A pays 8% simple interest for 10 years Investment B pays 7.75% compound interest for 10 years. Both require an initial $10,000 investment. The future value of A minus the future value of B...