A matrix A ∈ R^n,n is said to be continuous-time extended superstable (which we denote by A ∈ E_c) if there exists d ∈ Rⁿ such that

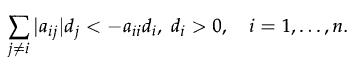
Similarly, a matrix A ∈ R^n,n is said to be discrete-time extended super stable (which we denote by A ∈ E) if there exists d ∈ Rⁿ such that

If A G Ec, then all its eigenvalues have real parts smaller than zero, hence the corresponding continuous-time LTI system x = Ax is stable. Similarly, if A £ E^, then all its eigenvalues have moduli smaller than one, hence the corresponding discrete-time LTI system x(k + 1) = Ax(k) is stable. Extended superstability thus provides a sufficient condition for stability, which has the advantage of being checkable via feasibility of a set of linear inequalities.
1. Given a continuous-time system x = Ax + Bu, with x £ R n, u £ Rm, describe your approach for efficiently designing a statefeedback control law of the form u = — Kx, such that the controlled system is extended superstable.
2. Given a discrete-time system x(k + 1) = Ax(k) + Bu(k), assume that matrix A is affected by interval uncertainty, that is

where â_ij is the given nominal entry, and 6ij is an uncertainty term, which is only known to be bounded in amplitude as for

given r_ij ≥ 0. Define the radius of extended superstability as the largest value ρ* of ρ ≥ 0 such that A is extended super stable for all the admissible uncertainties. Describe a computational approach for determining such a ρ*.

lajd; 0, i = 1,...,n.