A network of n = 6 peer-to-peer computers is shown in Figure 16.17. Each computer can upload or download data at a certain rate on the connection links shown in the figure.

Let b + ∈ R⁸ be the vector containing the packet transmission rates on the links numbered in the figure, and let b^– ∈ R⁸ be the vector containing the packet transmission rates on the reverse links, where it must hold that b⁺  ≥ 0 and b^– ≥ 0. Define an arc-node incidence matrix for this network

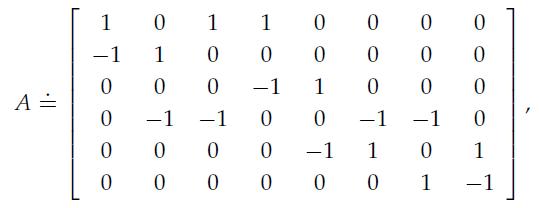
and(the positive part of A), (the negative part of A). Then, the total output (upload) rate at the nodes is given by  The net outflow at nodes is hence given by 

and the flow balance equations require that [v_net]_i = f_i, where f_i = 0 if computer i is not generating or sinking packets (it just passes on the received packets, i.e., it is acting as a relay station), f_i > 0 if computer i is generating packets, or f_i i. Each computer can download data at a maximum rate of v̅_dwl = 20 Mbit/s and upload data at a maximum rate of v̅_upl = 10 Mbit/s (these limits refer to the total download or upload rates of a computer, through all its connections). The level of congestion of each connection is defined as

Assume that node 1 must transmit packets to node 5 at a rate f₁ = 9 Mbit/s, and that node 2 must transmit packets to node 6 at a rate f₂ = 8 Mbit/s. Find the rate on all links such that the average congestion level of the network is minimized.

A = 001000 0 1 0 1 1 0 0 0 0 -1 0 0 0 1 -1 0 0 -1 -1 0 0 0 0 0 HOTOOO 0 0 0 - 1 0 0 1 000710 0 0 -1 -1 101000 -1 0 0 0 1